Le quaternaire pythagoricien connu sous le nom de Tétractys dévoile une formule numérique significative :

1 + 2 + 3 + 4 = 10

Cette équation illustre la relation directe entre le dénaire et le quaternaire.

Les Pythagoriciens accordaient une importance particulière à cette relation, en témoignait leur serment solennel « par la sainte Tétractys ». Moins connue, une autre formule de serment faisait référence au « carré de quatre » (4²=16), et il existe un lien évident entre les deux, le nombre quatre étant leur base commune. Cette observation nous conduit à envisager que la doctrine pythagoricienne présentait un caractère plus « cosmologique » que purement métaphysique, un trait que l’on retrouve souvent dans les traditions occidentales, y compris dans l’hermétisme.

Cette déduction peut sembler étrange à ceux qui ne sont pas familiers avec l’usage du symbolisme numérique. En effet, le quaternaire est universellement considéré comme le nombre propre à la manifestation cosmique, marquant ainsi le point de départ même de la « cosmologie ».

En revanche, les nombres qui le précèdent – l’unité, le binaire et le ternaire – sont strictement liés à l’ « ontologie ». Ainsi, la mise en avant particulière du quaternaire met en lumière le point de vue « cosmologique » lui-même.

Au début des Rasâ’il Ikhwân al-Safâ’ (Les Épîtres des Frères en pureté), les quatre éléments fondamentaux du quaternaire sont énumérés comme suit :

1. 1. 1. Le Principe, désigné sous le nom d’El-Bârî (البارئ), le « Créateur » (ce qui indique qu’il ne s’agit pas du Principe suprême, mais seulement de l’Être en tant que principe premier de la manifestation, qui est l’Unité métaphysique) ;
      2.  L’Esprit universel ;
      3. L’Âme universelle ;
      4. La Hylè primordiale.

La Hylè – Hiyulih (Homer Hiyulih – חומר היולי) est la matière céleste à partir de laquelle toute Création et toute naissance : l’éternité est l’un des attributs de Dieu, qui est le premier supérieur de tous, le causa prima de toutes causes ; les Mondes célestes et spirituels avant la Création étaient dépourvus de matérialité.
Le Hiyulih est le « pilier » de la théorie sur la modalité spirituelle dans la Création car c’est l’axiome de « potentiel et réalisation » :
« Entre le potentiel et le concret se trouve la force Hiyuli. Avant qu’une chose ne devienne une chose, elle existe de manière potentielle. Pour passer du potentiel au concret, il faut d’abord passer par l’étape intermédiaire de Hiyuli. De cette façon, toute la réalité émerge du Hiyuli. Par conséquent, le Hiyuli est la source de toute Création » — Nahman de Bratslav
Ainsi donc, la providence divine a opéré une sorte d'”individuation” en définissant la nature de toute créature, de tout être et de tout existant à partir de la Hylè, précisément du potentiel au acte.

Nous n’aborderons pas ici les différentes perspectives selon lesquelles ces termes pourraient être envisagés. On pourrait notamment les associer aux quatre “mondes” de la Kabbale hébraïque, qui trouvent également leur équivalent exact dans l’ésotérisme islamique.

Ce qui importe pour le moment, c’est que ce quaternaire ainsi constitué est considéré comme un présupposé de la manifestation, dans le sens où la présence de tous ses éléments est nécessaire au développement complet des possibilités qu’elle contient.

De ce fait, on retrouve toujours spécifiquement la marque ou « signature » du quaternaire dans l’ordre des choses manifestées. Cela se manifeste, par exemple, à travers les quatre éléments (en excluant l’Éther, car il s’agit des éléments « différenciés »), les quatre points cardinaux (ou les quatre régions spatiales qui leur correspondent, avec les quatre “piliers” du monde), les quatre phases naturelles dans lesquelles tout cycle se divise (les âges de la vie humaine, les saisons de l’année, les phases lunaires du mois, etc.). Cette tendance se répète à l’infini, permettant ainsi de déduire une multitude d’applications du quaternaire, toutes reliées entre elles par des correspondances analogiques rigoureuses. En réalité, elles ne sont que des aspects plus ou moins spécifiques d’un même « schéma » général de la manifestation.

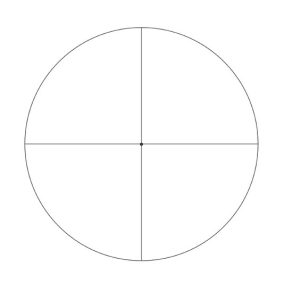Ce « schéma », dans sa forme géométrique, est l’un des symboles les plus répandus, véritablement partagé par toutes les traditions. Il s’agit du cercle divisé en quatre parties égales par une croix formée de deux diamètres perpendiculaires. On peut immédiatement remarquer que cette figure exprime précisément la relation entre le quaternaire et le dénaire, telle que la formule numérique que nous avons mentionnée précédemment. En effet, le carré représente géométriquement le quaternaire lorsqu’il est considéré dans son aspect « statique ».

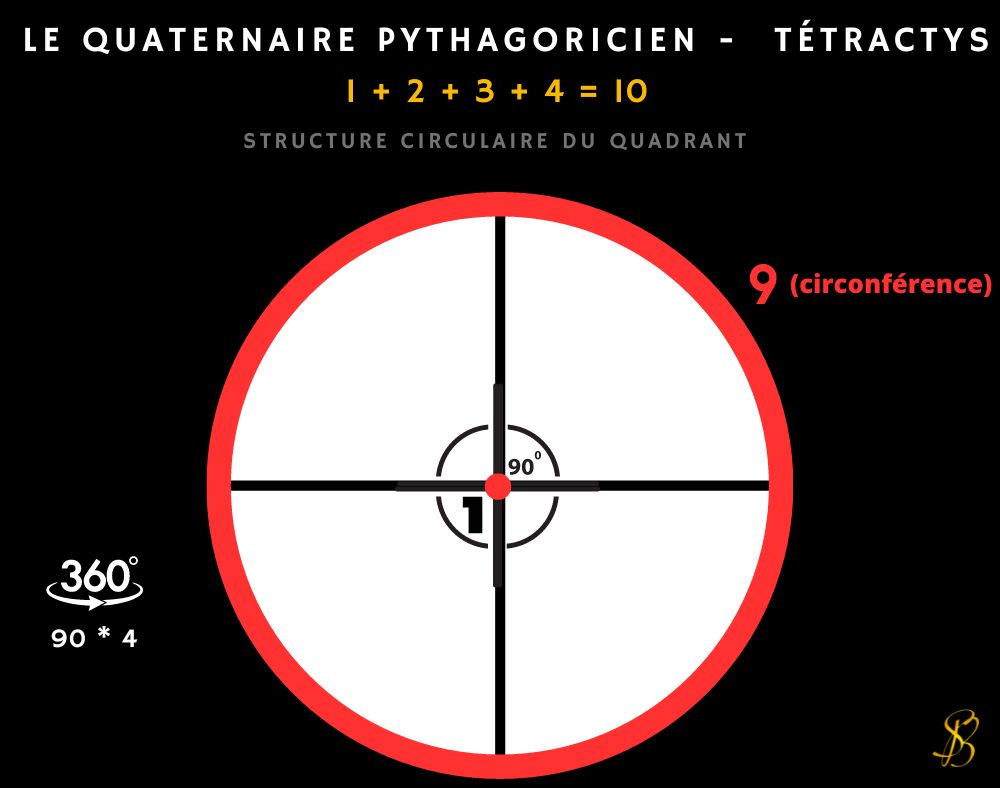
Cependant, dans son aspect « dynamique », il est représenté par la croix. Lorsque cette croix tourne autour de son centre, elle engendre la circonférence, qui, avec le centre, représente le dénaire, qui, comme nous l’avons dit auparavant, est le cycle numérique complet. Cela correspond à ce qu’on appelle la « Structure circulaire du quadrant », qui est la représentation géométrique de ce que la formule arithmétique 1 + 2 + 3 + 4 = 10 exprime.

Inversement, le problème hermétique de la « quadrature du cercle »  (expression souvent mal comprise) n’est rien d’autre que la division quaternaire du cercle préalablement donné par les deux diamètres perpendiculaires. Numériquement, cela se traduit par la même formule, mais écrite en sens inverse : 10 = 1 + 2 + 3 + 4. Cela démontre que tout le développement de la manifestation est ainsi ramené au quaternaire fondamental.

Cependant, revenons à la relation entre la Tétractys et le carré de quatre (4²=16) : les nombres 10 et 16 occupent tous deux le même rang, à savoir le quatrième, respectivement dans la série des nombres triangulaires et celle des nombres carrés.

Les nombres triangulaires sont obtenus en effectuant la somme des nombres entiers consécutifs depuis l’unité jusqu’à chaque terme successif de la série. L’unité elle-même est à la fois le premier nombre triangulaire et le premier nombre carré, car elle est à la fois le principe et l’origine de la série des nombres entiers, et donc également de toutes les autres séries qui en découlent. Le deuxième nombre triangulaire est 1 + 2 = 3, ce qui montre que dès que l’unité produit le binaire par sa propre polarisation, le ternaire en découle immédiatement. Ceci est évident dans sa représentation géométrique : 1 correspond au sommet du triangle, 2 aux extrémités de sa base, et le triangle lui-même, dans son ensemble, représente naturellement le nombre 3.

En considérant ensuite les trois termes du ternaire comme ayant une existence indépendante, leur somme donne le troisième nombre triangulaire : 1 + 2 + 3 = 6. Étant le double du ternaire, ce nombre sénaire peut être considéré comme impliquant un nouveau ternaire qui reflète le premier, comme dans le symbole bien connu du « sceau de Salomon ».

En poursuivant la série, le quatrième nombre triangulaire est obtenu en faisant la somme de 1 + 2 + 3 + 4, ce qui donne 10, c’est-à-dire la Tétractys. Comme nous l’avons déjà expliqué, cela démontre que le quaternaire contient d’une certaine manière tous les nombres, car il contient le dénaire. Cela rejoint la formule du Tao-te-King : « un a produit deux, deux a produit trois, trois a produit tous les nombres ». Cela revient à dire que toute la manifestation est comme enveloppée dans le quaternaire, ou inversement, que le quaternaire constitue la base complète de son développement intégral.

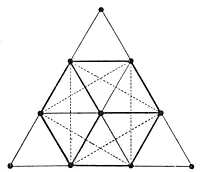
La Tétractys, en tant que nombre triangulaire, était représentée par un symbole qui avait une forme globale ternaire, avec quatre éléments sur chaque côté extérieur. Ce symbole se composait au total de dix éléments, représentés par autant de points, dont neuf étaient situés sur le périmètre du triangle et un au centre. Il est intéressant de noter que malgré la différence de forme géométrique, on retrouve une équivalence avec la représentation du dénaire par le cercle, où 1 correspond au centre et 9 à la circonférence. À ce sujet, il est également pertinent de mentionner que c’est parce que 9, et non pas 10, est le nombre de la circonférence, que celle-ci est divisée normalement en multiples de 9 (90 degrés pour le quadrant, et par conséquent 360 pour la circonférence entière), ce qui est directement lié à la question des « nombres cycliques ».

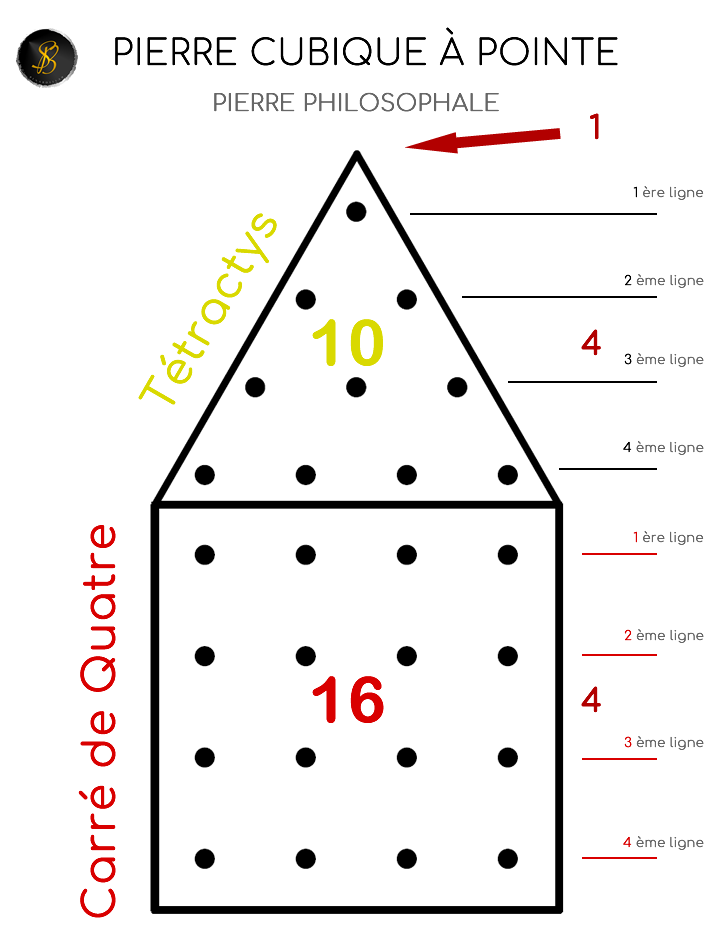
Le carré de quatre est géométriquement un carré dont les côtés comprennent quatre éléments, tout comme ceux du triangle que nous avons mentionné précédemment. Si l’on considère que les côtés sont mesurés par le nombre de ces éléments, on en déduit que les côtés du triangle et du carré seront égaux. On peut alors superposer les deux figures en faisant correspondre la base du triangle au côté supérieur du carré, comme illustré dans le schéma suivant (où les points sont marqués à l’intérieur des figures pour plus de clarté, permettant de compter distinctement ceux qui appartiennent respectivement au triangle et au carré). Cette combinaison des deux figures donne lieu à plusieurs remarques importantes.

Tout d’abord, si l’on considère uniquement le triangle et le carré en tant que tels, cet ensemble représente géométriquement le septénaire, puisque celui-ci est la somme du ternaire et du quaternaire : 3 + 4 = 7. Plus précisément, selon la disposition même de la figure, ce septénaire est formé de l’union d’un ternaire supérieur et d’un quaternaire inférieur, ce qui peut avoir différentes applications. Dans notre contexte particulier, il suffit de dire que, dans la correspondance entre les nombres triangulaires et les nombres carrés, les premiers doivent être associés à un domaine plus élevé que les seconds. Par conséquent, on peut en déduire que, dans le symbolisme pythagoricien, la Tétractys devait jouer un rôle supérieur à celui du carré de quatre. En réalité, tout ce que l’on sait à son sujet semble indiquer que cela était effectivement le cas.

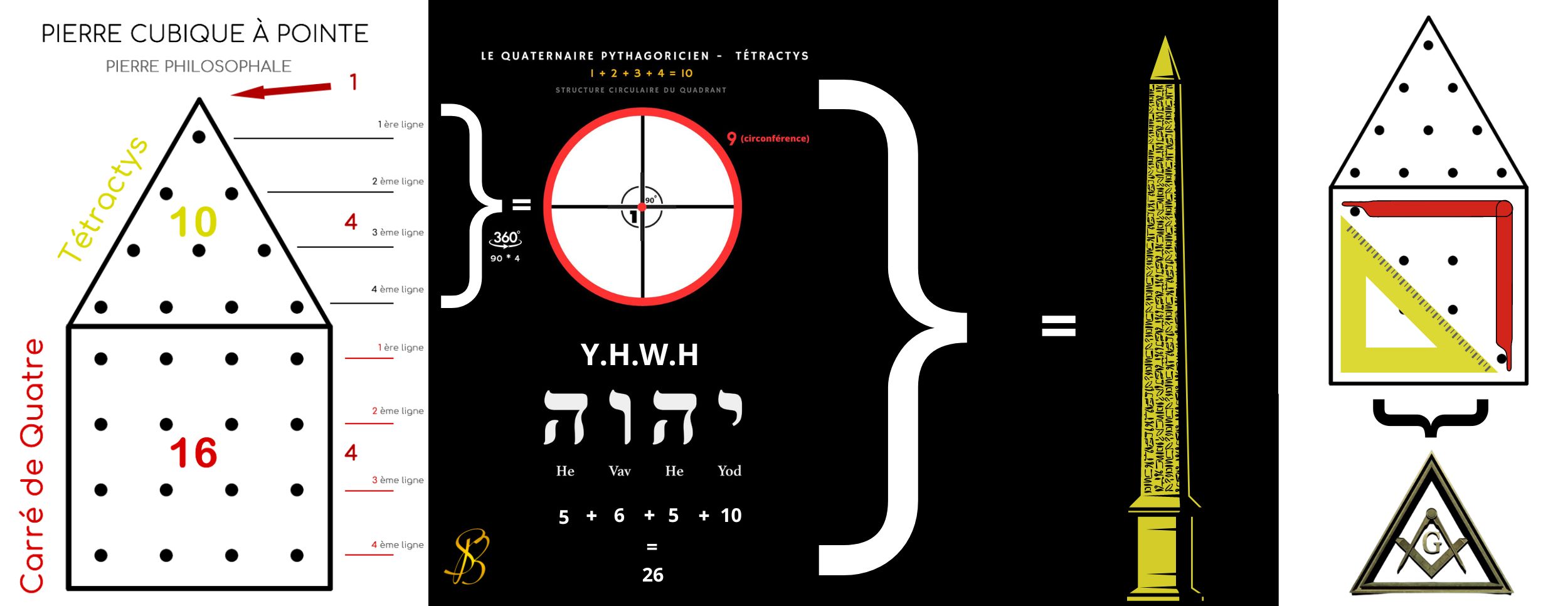
Maintenant, il y a autre chose de plus singulier, et qui, bien que se référant à une forme traditionnelle différente, ne peut certes pas être regardé comme une simple « coïncidence » : les deux nombres 10 et 16, contenus respectivement dans le triangle et dans le carré ont pour somme 26 ; or, ce nombre 26 est la valeur numérique totale des lettres formant le tétragramme hébraïque (Y.H.W.H), iod-hé-vau-hé. De plus, 10 est la valeur de la première lettre iod et 16 est celle de l’ensemble des trois autres lettres hé-vau-hé ; cette division du tétragramme est parfaitement normale, et la correspondance de ses deux parties est encore très significative : la Tétractys s’identifie ainsi au iod dans le triangle tandis que le reste du tétragramme s’inscrit dans le carré placé au-dessous de celui-ci.

D’autre part, le triangle et le carré contiennent l’un et l’autre quatre lignes de points ; il est à noter, bien que ceci n’ait en somme qu’une importance secondaire, et uniquement pour marquer encore les concordances de différentes sciences traditionnelles, que les quatre lignes de points se retrouvent dans les figures de la géomancie, figures qui d’ailleurs, par les combinaisons quaternaires de 1 et 2, sont au nombre de 16 = 4² ; et la géomancie, comme son nom l’indique, est en relation spéciale avec la terre, qui, suivant la tradition extrême-orientale, est symbolisée par la forme carrée.

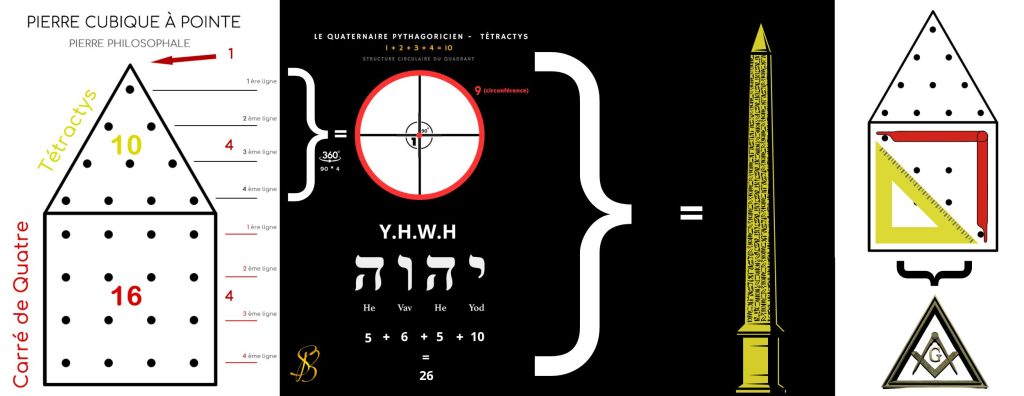
Enfin, si l’on considère les formes solides correspondant, dans la géométrie à trois dimensions, aux figures planes dont il s’agit, au carré correspond un cube, et au triangle une pyramide quadrangulaire ayant pour base la face supérieure de ce cube ; l’ensemble forme ce que le symbolisme maçonnique désigne comme la « pierre cubique à pointe », et qui, dans l’interprétation hermétique, est regardé comme une figure de la « pierre philosophale ». Il y a encore, sur ce dernier symbole, d’autres remarques à faire ; mais, comme elles n’ont plus de rapport avec la question de la Tétractys, il sera préférable de les envisager séparément.

Cet article est rédigé grâce à des sources d’informations variées telles que :  Wikipédia – Oswald Wirth – Jules Boucher – René Guénon, etc…